
bearbeitet: 10.01.2015
ergänzt: 24.03.2016
überarbeitet: 30.01.2021
Warum ist die Behauptung falsch, man könne Masse in Energie "umwandeln" und zurück?
Eine Erklärung von Dr. Manfred Pohl
Viele Physiker der heutigen Generation behaupten, man könne Energie in Masse umwandeln und zurück.
Einer sagte sogar auf meinen Einwand, dies sei "milliardenfach" bewiesen. Nun, indem man das einfach
mit Kraftausdrücken wie "milliardenfach" behauptet, kann man es nicht beweisen. "Milliardenfach" ist auch
gar nicht erforderlich. Mir genügte schon ein einziger Beweis, aber daran scheitert das Vorhaben. Die Verfechter
dieser Ansicht haben nämlich ganz einfach die Masse-Energie-Äquivalenz nicht verstanden. Sie gehen davon
aus, daß es reine, also masselose Energie gibt, die man aus einer Masse erzeugen könne. Und genau da
liegt der Fehler. Die Ursache für diese Fehlhaltung liegt in einem falschen Materiebegriff. Noch immer wird
an vielen Stellen in der gegenwärtigen Physik behauptet, die Energie gehöre nicht zur Materie, sie wird
aus der Materie herausgelöst und ihr gegenübergestellt. Dies führt letztendlich zu der Auffassung, man
könne das eine in das andere überführen.
Zur Richtigstellung analysiere ich zum Beispiel die Energiegleichung der mechanischen Energie:
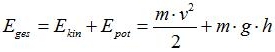
v, g und h sind in dieser Gleichung von Null verschiedene Werte. Aus der Gleichung geht hervor, daß stets ist die Energie Null ist, wenn die Masse Null ist. Das heißt, es gibt keine Energie ohne Masse. Auch aus der Einsteinschen Gleichung der Masse-Energie-Äquivalenz ergibt sich nichts anderes:
![]() .
.
c ist eine Naturkonstante, die Vakuumlichtgeschwindigkeit. Auch hierin
ist die Energie Null, wenn die Masse Null ist und umgekehrt.
Könnte man Masse in Energie "umwandeln", so hieße das, durch Annullierung einer Darstellungsform der Materie
eine andere zu erhalten, das hieße, Masse verschwindet, daraus entsteht Energie (die keine Masse beinhaltet!),
im umgekehrten Fall verschwindet Energie, aus ihr entsteht Masse (die frei von Energie ist!).
Folgende Überlegung zeigt die Unmöglichkeit eines solchen Vorganges.
Ausgangspunkt ist der Energieerhaltungssatz: In einem geschlossenen System ist die Gesamtenergie konstant,
wenn nicht aus dem System Energie nach außen abgeführt oder von außen Energie dem System zugeführt wird:
![]() (1)
(1)
Teilt man die Gesamtenergie in zwei beliebige Teile auf, etwa
![]() (2)
(2)
so ist folglich wegen (1)
![]() (3)
(3)
Ich folge nun der falschen Annahme, man könne Energie in Masse umwandeln: Es werde der Energieanteil E1 in die Masse m umgewandelt:
![]() (4)
(4)
Unter dieser Annahme wäre nun der Energieanteil E1 nicht mehr vorhanden, an seiner Stelle ist die Masse m entstanden. Verwendet man nun (4) in (3), so entsteht
![]() (5)
(5)
Schaut man auf die Gleichung (5), stellt man fest, daß bereits die Maßeinheiten nicht stimmen.
Man kann Größen mit verschiedenen Maßeinheiten nicht addieren oder voneinander subtrahieren. So kann man
auch J und kg nicht addieren. Sonst müßte man auch einen Meter und eine Sekunde addieren können.
Das alles ist völliger Unsinn. Wir wollen nun vorübergehend über diesen Mangel hinwegsehen und an der Behauptung
festhalten, man könne eine solche Umwandlung ausführen. Dann wäre, wie Gleichung (5) ausweist, die Summe
von Energie und Masse konstant. Das bedeutet, daß eine größere Masse eine kleinere Energie enthält und
eine kleinere Masse eine größere.
Entsprechend der Masse-Energie-Äquivalenz ergibt sich aber eine ganz andere Aussage mit einem völlig
anderen Ergebnis.
Das Masse-Energie-Äquivalent lautet
![]() (6).
(6).
Hierin ist c die Naturkonstante Vakuumlichtgeschwindigkeit.
Das bedeutet folglich, daß
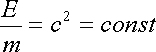 (7).
(7).
ist. Das heißt, das Verhältnis von Energie zu Masse ist konstant (nicht die Summe!). Also eine
Vergrößerung der Masse führt zur Erhöhung der Energie und umgekehrt. Dies ist
aber eine gänzlich andere Aussage wie in Gleichung (5), der völlig unsinnigen Summe
![]() ,
in der sich bei Vergrößerung der Masse eine kleinere Energie ergeben müßte.
,
in der sich bei Vergrößerung der Masse eine kleinere Energie ergeben müßte.
Da nun aber in der obigen Ableitung die Ausdrücke (1), (2) und (3) korrekt abgeleitet worden sind, muß sich
der Fehler somit im Ausdruck (4) befinden, in welchem die "Umwandlung" von Energie in Masse postuliert wurde.
Dieser Schritt ist nicht möglich. Einen solchen Vorgang gibt es in der Natur nicht. Man kann eben
J nicht in kg umwandeln oder umgekehrt, genauso, wie man beispielsweise kWh nicht in
m2 "umwandeln" kann. Das ist physikalisch Unsinn. Deshalb ist
das Ergebnis der Gleichung (5) also offenkundig falsch.
Analysieren wir nun genauer die Maßeinheiten, die wir oben vorübergehend außeracht gelassen hatten.
Masse und Energie sind nicht addierbar. Es sind zwei wesensunterschiedliche Entitäten, von denen, nebenbei bemerkt,
die eine nicht ohne die andere vorhanden sein kann, was aus der Gleichung (6) hervorgeht: Wenn die Masse
m = 0 ist, so ist auch E = 0. Ist aber E ǂ 0, so ist auch m ǂ 0, das heißt,
es gibt keine Masse ohne Energie und keine Energie ohne Masse.
Diese beiden Entitäten haben verschiedene Maßeinheiten. Die Maßeinheit der Masse ist das kg:
![]()
Die Maßeinheit der Energie ist das Joule (mkg2/s2):
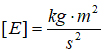
Physikalische Kategorien mit verschiedenen Maßeinheiten kann man nicht addieren. Was ergäbe die Addition eines Kilogramms mit einem Joule? Man müßte schreiben
![]()
Diese "Summe" ist nicht erklärbar. Ein anderes Beispiel: Was ergäbe zum Beispiel die Addition eines
Meters mit einer Sekunde? Eine solche Addition ist physikalisch unsinnig. Ebenso unsinnig, als wolle man 3 Stühle
und 4 Hühner addieren.
Setzt man hingegen die Maßeinheiten in das Masse-Energie-Äquivalent ein, so erhält man
![]() .
.
Wie man sieht, ein korrektes Ergebnis.
Ein Beispiel aus der Elektrotechnik: Das Verhältnis von Spannung zu Strom ist der Widerstand. Die Maßeinheiten
der Größen sind das Volt, das Ampere und das Ohm:
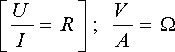 .
.
Niemand vom Fach käme auf die Idee, Spannung und Strom zu addieren (U + I = ?), denn es wäre ohne Sinn.
Beim Einsetzen der Einheiten aus dem MKSA-System in die Gleichung
![]()
erhält man ebenfalls ein völlig korrektes Ergebnis, während die Summe
![]()
ohne physikalischen Inhalt ist. Genauso verhält es sich mit der Masse und der Energie. Man kann beide physikalische
Kategorien nur so behandeln, wie es ihre natürlichen Eigenschaften zulassen. Verletzt man dieses Prinzip,
so erhält man keine oder unbrauchbare Ergebnisse.
Fazit:
Man kann Energie nicht in Masse "umwandeln". Auch der umgekehrte Vorgang ist physikalisch unsinnig. Beide
Entitäten sind zwei Erscheinungsformen ein und derselben Realität, der Materie. Es kann die eine nicht ohne
die andere auftreten. Wo Energie ist, ist auch Masse, und wo Masse ist, ist auch Energie. Das ist die Aussage
der Masse-Energie-Äquivalenz.
Ein Physiker, der die "Umwandlung" der Masse in Energie und umgekehrt propagiert, hat ernsthaften Nachholbedarf
im Erlernen der elementaren Grundkenntnisse der Physik.