
bearbeitet: 29.05.2005
ergänzt: 14.03.2012
Der sogenannte "Body Mass Index"
und der grundsätzliche Irrtum
Eine Kurzdarstellung
In der Medizin wird versucht, die Körperfülle eines Menschen (die Figur) mit Hilfe des sogenannten "Body
Mass Index", abgekürzt BMI, in Zahlen zu bewerten. Dies geschieht mit mäßigem Erfolg und ohne die Möglichkeit
eines objektiven Vergleichs unterschiedlicher Personengruppen. Die Ursachen dafür liegen in der fehlerhaften
Grundkonzeption der Maßzahl, die auf einer falschen Prämisse fußt. Der "Body Mass Index" ist so
unzweckmäßig wie seine Bezeichnung. Als Maß für die Beurteilung der Körpermasse oder der Körperfülle eines
Menschen ist er ungeeignet. Der Beitrag soll dafür den Beweis antreten und einen Ausweg aus dem Dilemma
zeigen.
Für die Beurteilung der Figur (Statur, Körperfülle) einer Person, eines Lebewesens oder eines Körpers allgemein wird
ein Zusammenhang benötigt, der bei gleicher Figur für verschiedene Körpergrößen eine Konstante ergibt. Der
sogenannte BMI, bei dem die Masse des Körpers durch das Quadrat der Körpergröße dividiert wird, ergibt eine
solche Konstante nicht. Bei gleicher Figur und unterschiedlicher Größe entstehen stets verschiedene Werte.
Der Ansatz für den BMI ist in seinem Grundsatz falsch. Dies ist nach rein geometrischen Überlegungen auch zu
erwarten, denn die Masse eines beliebigen Körpers ist seinem Volumen proportional und nicht einem fiktiven
Flächenäquivalent. Der Proportionalitätsfaktor ist die mittlere Dichte des Materials, aus dem
der Körper besteht.
| m = V * d | mit m - Masse [kg] und d - Dichte [kg/m3] |
Geht man nun davon aus, daß sich die mittlere Dichte der Körpermassen verschiedener Menschen
nur in vernachlässigbar kleinen Größen unterscheidet, kann man sich bei den weiteren
Untersuchungen auf die Zusammenhänge zwischen Volumen und Längenausdehnung
beschränken.
Das Volumen eines Körpers ist aber stets eine Funktion der dritten Potenz seiner Längenausdehnung. Im
kartesischen Koordinatensystem (x,y,z) läßt sich darstellen
| V = f(x,y,z) [m3] |
Dies sei in einfachster Form an einem Würfel gezeigt. Es ist
V = a3 mit V - Volumen, a - Kantenlänge.
Nun sei a1 = a/2 die Kante eines Würfels mit der halben Kantenlänge. Sein Volumen ist
V1 = a13 = a3/8 = V/8.
Folglich ist
V/a3 = V1/a13 = const.
Hingegen ist
V/a2
![]() V1/a12, denn
V1/a12, denn
V1 = V/8 aber
a12 = a2/4.
Für anders geformte Körper ist dies genauso, wenn bei der Änderung der Raumdimensionen deren Verhältnisse
Länge/Breite und Länge/Höhe konstant bleiben - trivial: Wenn der geänderte Körper und der Ausgangskörper
ähnlich sind. Aus den bisherigen Überlegungen folgt:
Die Masse eines geometrischen Körpers ist für gleiche Materialdichten proportional dem Kubik einer beliebigen
seiner drei Raumdimensionen. Für die weiteren Untersuchungen wird wegen der direkten Proportionalität
von Masse zu Volumen nur das Volumen betrachtet.
Zwei Beispiele:
1. Ein Quader habe die Kantenlängen a, b und c. Das Volumen des Quaders ist daraus
V = a * b * c.
Werden nun die Kantenlängen des Quaders um den Faktor k verändert, so daß der neu entstehende Körper dem Ausgangskörper ähnlich ist, also
a1 = a * k,
b1 = b * k,
c1 = c * k.
So entsteht
V1 = a1 * b1 * c1 = a * b * c * k3 = V * k3.
2. Ein Kegel mit kreisförmiger Grundfläche habe den Radius des Grundkreises r und die Höhe h. Sein Volumen ist daraus
V = π r2 * h / 3
Die Längen r und h werden um den Faktor k geändert.
r1 = k * r
h1 = k * h.
So entsteht
V1 = π r1 2 * h1 / 3 = π r2 * k2 * h * k / 3 = V * k3.
Allgemein ist für einen beliebigen Körper
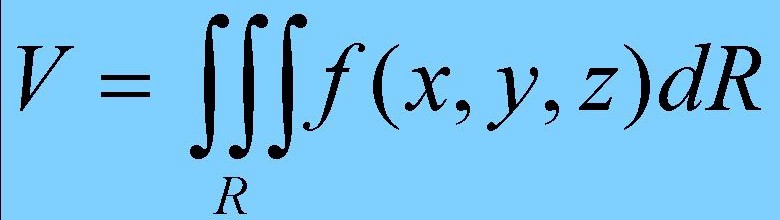
Hierin ist f(x,y,z) die Funktion, die das zu integrierende Raumgebiet beschreibt. dR ist das Raumelement, nach dem im Raumgebiet f(x,y,z) integriert wird. Dieses Raumelement ist, dargestellt im kartesischen Koordinatensystem, das Produkt der Längenelemente dx*dy*dz in den drei Raumkoordinaten. Läßt die Raumfunktion f(x,y,z) eine Trennung in die drei kartesischen Ebenen zu, kann das Raumintegral auch in drei nacheinander ausführbare Integrationen über je eine der linearen Integrationsvariablen zerlegt werden.
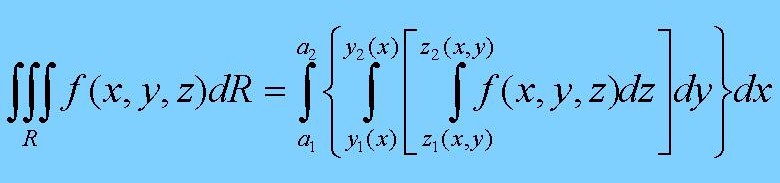
Hieraus ist auch für einen allgemeinen Körper die Proportionalität des Volumens zur dritten Potenz einer
Längenausdehnung erkennbar. Natürlich ist das Raumintegral auch in anderen Koordinatensystemen
darstellbar, zum Beispiel im zylindrischen oder im sphärischen. Die Geometrie ist dennoch die
gleiche, sie ist nur etwas schwieriger zu erklären.
Durch diesen Ansatz ist erreicht worden, daß für beliebige geometrische Körper ein Faktor ermittelt werden kann, der
die Figur dieses Körpers eindeutig charakterisiert, weil er von der Größe des Körpers unabhängig ist. Dieser Faktor sei
mit F bezeichnet, er hat den Wert
| F = m/l3 |
Ich nenne ihn Figurfaktor eines Körpers.
Angewendet auf den Menschen ist dieser Faktor mit m - Körpermasse und l - Körpergröße
ein Maß für die Figur (Statur oder Körperfülle), unabhängig von seiner Größe oder etwa seinem Alter. Für die gleiche figürliche
Gestalt ergibt sich stets der gleiche Faktor.
Mit dem Figurfaktor ergeben sich nun objektive Vergleichsmöglichkeiten für die Körperfülle von Menschen
verschiedener Körpergröße. So kann zum Beispiel ein Mensch der Größe 1,80 m und einer Masse von 80 kg als
normalgewichtig angesehen werden. Er hat einen Figurfaktor von
F = 80 / 1,83 = 13,72.
Wieviel sollte nun ein Mensch von der gleichen Körperfülle wiegen, wenn er 1,60 m groß ist? Man erhält
m = F * l3 = 13,72 * 1,63 = 56,2 kg.
Wie groß ist ein Mensch von der gleichen Körperfülle, der 70 kg wiegt? Es ergibt sich
70 = 13,72 * l3 daraus
l = 1,72 m.
Der sogenannte Body-Mass-Index läßt solche Vergleiche nicht zu. An obigem Beispiel ist das zu sehen. Die drei Personen mit der gleichen Figur haben ganz verschiedene BMI:
80 / 1,82 = 24,7,
56,2 / 1,62 = 22,0,
70 / 1,722 = 23,7.
Um diese Diskrepanzen auszugleichen, muß man unbegründete Korrekturen einführen, wie zum Beispiel eine Abhängigkeit vom Alter oder andere willkürliche Eingriffe. Es ist nicht zu erwarten, daß man mit derart empirischen Abwandlungen die Unordnung in dem System aufheben kann. Die Objektivität der Maßzahl ist in keiner Weise gegeben. Dies wissen auch die Autoren und die Anwender, denn alle geben zu ihren berechneten BMI-Werten umfangreiche und umständliche Tabellen oder Grafiken hinzu, mit denen die Rechenwerte dann manipuliert, diskutiert und interpretiert werden, bis vom eigentlichen Rechenwert kaum noch etwas übrig ist. In den verschiedensten Internetbeiträgen, die es zu Tausenden gibt, findet man ganz unterschiedliche Ausdeutungen der berechneten Werte. In manchen Beiträgen findet man ausgemachten Unfug vor, wie zum Beispiel
Body Mass Index = Körpergewicht in kg / Körpergröße in m2 (!),
Auch sprachlich gibt dieser sogenannte BMI Anlaß zur Kritik. Wozu brauchen wir, wenn wir uns deutsch unterhalten,
für die Beschreibung eines Problems eine englische Bezeichnung? Man kann solche Marotten nur in die heute
weit verbreitete Mode zur Wichtigtuerei und zu angeberischem Auftreten einordnen. Wenn dann solche unnützen
Anglizismen auch noch wie hier mit fachlicher und sachlicher Inkompetenz einhergehen, ist die Mißleistung der
Schöpfer ausreichend dokumentiert.
Die Aufgabe der Medizin erschöpfte sich nun darin, sinnvolle Einteilungen für den Figurfaktor zu erarbeiten,
um beispielsweise Untergewicht, Normalgewicht, leichtes Übergewicht, erhebliches Übergewicht, Fettleibigkeit
- oder aber andere Kategoriedefinitionen - zu unterscheiden. Die vorgenommene Kategorisierung gilt dann aber
für alle Menschen beliebiger Größe und beliebigen Alters. Es sind keine Kunstgriffe oder empirischen Manipulationen
mehr nötig, um den Faktor zur Erhaltung seiner Aussagekraft zu korrigieren. Man kann nun endlich durch
weiterführende Forschungen auch herausfinden, ob zum Beispiel gleichgroße Männer und Frauen
unterschiedliche Figurfaktoren haben müssen, und wenn ja, worin die Unterschiede begründet sind.
Oder man kann zum Beispiel statistisch herausfinden, ob es gravierende Unterschiede in der Figurgestaltung von
Kindern und Erwachsenen gibt. Der Figurfaktor bietet ein objektives Vergleichsmaß. Mit dem sogenannten
BMI sind solche Fragen nicht bewertbar, da in seiner Grundkonzeption falsche Zusammenhänge implementiert
sind, die jede Aussage strukturell verfälschen.
Ich arbeite im privaten Bereich seit mehreren Jahren mit den Kategorien der nachfolgenden Tabelle.
| Figurfaktor | Beschreibung |
| F<10 | Magerkeit |
| 10<=F<12 | Untergewicht |
| 12<=F<14 | Normalgewicht |
| 14<=F<16 | geringes Übergewicht |
| 16<=F<18 | erhebliches Übergewicht |
| 18<=F | Fettleibigkeit |
Nach Einschätzung aller Beteiligten treffen die Werte im wesentlichen zu. Jedoch habe ich in meinem Umfeld für die erste
und die letzte Tabellenzeile keine verfügbaren Beispielpersonen, an denen solche Meßwerte aufgenommen werden konnten.
Aber es lassen sich alle 12 Erwachsenen und 10 Kinder verschiedenen Alters, mit denen regelmäßige Messungen
durchgeführt werden, mit allgemeiner Akzeptanz in diese Kategorien eingliedern. Auch einzelne andere Personen, von denen
gelegentliche Meßwerte genommen wurden, bestätigten intuitiv die Brauchbarkeit der angegebenen Grenzen. Sicher
ist die Tabelle streitbar, denn ich bin kein Mediziner. Strittige Fragen könnten jedoch mit hoher Wahrscheinlichkeit nur die aufgestellten
Bereichsgrenzen oder die Zweckmäßigkeit und die Zahl der verbalen Gruppenbenennungen betreffen. Zusätzliche
Korrekturbedingungen oder andere Abhängigkeiten werden nicht erforderlich sein.
Die gesamte Arbeit befindet sich hier.