
bearbeitet: 10.11.2004
Bemerkungen über den Fußball
Leute, die mich kennen, werden sicher sagen: "Pohl und Fußball? Das geht doch gar nicht zusammen". Im Grunde richtig.
Fußball ist eine Sache, um die ich mich kaum kümmere. Es sei denn, es sind politische oder aber wissenschaftlich-theoretische
Themen zu behandeln. Beides soll in diesem Beitrag gemacht werden.
So fange ich - nur ganz kurz gehalten - mit einer politischen Frage an. Die große Popularität des Fußballsports und die
Möglichkeit, aus dieser Popularität Geld abzuleiten, hat bedauerlicherweise in den letzten 20 bis 30 Jahren dazu geführt, daß
die Sportart des Sportes beraubt wurde und fast ausschließlich nur noch Kommerz ist. Ist nicht für jedermann sichtbar, daß
gerade beim Fußball jegliches Augenmaß für das Verhältnis von Aufwand zu Leistung verlorengegangen ist? Fußballer, die eine
bestimmte Spielhöhe erreicht haben, erhalten Zuwendungen, die die Grenzen der Normalität weit überschreiten. Die Summen,
die für die Ablösung guter Spieler und deren Übernahme in andere Vereine fließen, lassen einen Ruch von Menschenhandel nicht
mehr vermeiden. So überspannt wie diese Geldgrößen sind dann auch die Verhaltensweisen derjenigen, die sich damit befassen.
So ist es heute im allgemeinen üblich - die Zeitungen sind fast täglich voll davon - daß beim Verlieren eines oder zweier Spiele einer
Mannschaft der Trainer gefeuert wird. Kurios. Spieler werden selten entlassen, nur immer Trainer. Da fragt man sich doch, wer auf
dem Rasen eigentlich spielt. Unter dem Eindruck dieser Alltäglichkeiten war es wahrlich wohltuend zu lesen, daß Hansa Rostock
seinen Trainer Juri Schlünz auf gar keinen Fall entlassen werde, auch wenn es mal nicht so gut liefe. Ja - und drei Tage später
mußte ich dann vernehmen, daß er zurückgetreten ist. Man versteht das einfach nicht. Meistens nämlich ist
der Trainer gar nicht schuld, wenn verloren wird. Es mag unglaubhaft klingen, aber auch die Spieler sind nicht immer daran schuld. Wer denn
dann? Sehen Sie, mit dieser Frage kommen wir wie von selbst zu den wissenschaftlich-theoretischen Fragen.
Ich will einmal analysieren, welche Faktorengruppen den Ausgang eines Fußballspiels bestimmen. Es sind zwei, die sich grundsätzlich
unterscheiden:
Die Faktorengruppe A beeinflußt den Spielausgang bewertbar bzw. berechenbar.
Die Faktorengruppe B beeinflußt den Spielausgang sporadisch positiv oder negativ. Der Einfluß entzieht sich aber
weitgehend einer voraussehbaren Beurteilung und einer zielgerichteten Veränderung durch Spieler oder Trainer.
Die beiden Faktorengruppen sollen auf einer Achse dargestellt werden, die nach rechts ansteigend ein relativiertes
Leistungspotential L abbildet.

Die Faktorengruppe A ergibt für eine Mannschaft auf der Leistungsachse einen berechenbaren bzw. meßbaren Punkt.
Die Faktorengruppe B ergibt in einer zu schätzenden Streuungsbreite um diesen Punkt einen Bereich der Abweichung vom
Leistungspotential durch die zufälligen Einflüsse auf den Spielablauf, die sich positiv oder negativ auswirken können.

Das augenblickliche wahrscheinliche Leistungspotential liegt also um den Punkt L1 zwischen A1 und B1.
Setzt man nun eine zweite Mannschaft, die ein sehr viel höheres Leistungspotential hat, auf diese Achse und setzt voraus,
daß die Mannschaft mit dem höheren Leistungspotential siegen wird, so ergibt sich das nachfolgende Bild:
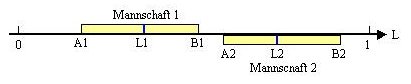
Die Mannschaft 2 wird also siegen, weil sie unter Berücksichtigung aller Zufallsfaktoren in jedem Fall das höhere
Leistungspotential hat. Natürlich muß man festhalten, daß so große Leistungsunterschiede in der
Praxis kaum vorkommen. Allenfalls nur dann, würde eine Schülermannschaft gegen die Bundesliga antreten.
Im Regelfall liegen die Leistungspotentiale L1 und L2 wesentlich dichter beieinander.
Verringert man nun den Abstand zwischen den Leistungspotentialen beider Mannschaften, so ergeben sich nachfolgende
mögliche Bilder:
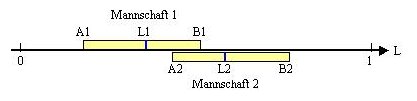
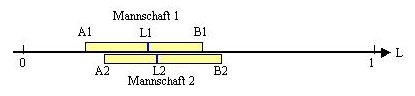
Es kommt zu Überschneidungen der augenblicklichen Leistungspotentiale beider Mannschaften im Bereich zwischen
A2 und B1. In diesem Bereich ist der Sieg der Mannschaft 2 nicht sicher vorhersehbar. Deutlicher gesagt, der Sieg der Mannschaft 2
ist nicht garantiert. Im Volksmund sagt man dazu, der Ball ist rund, es kann viel passieren. Es muß mit Wahrscheinlichkeiten
des Sieges der einen oder der anderen Mannschaft gerechnet werden. Um diese Wahrscheinlichkeiten darzustellen, seien folgende
Bezeichnungen verwendet:
Die Gesamtbreite des augenblicklichen Leistungssprektrums der Mannschaft 1: B1 - A1 = a.
Die Gesamtbreite des augenblicklichen Leistungssprektrums der Mannschaft 2: B2 - A2 = b.
Die Überschneidungsgröße der augenblicklichen Leistungssprektren: B1 - A2 = u.
Normiert auf die Gesamtbreite des augenblicklichen Leistungspotentials errechnen sich die Wahrscheinlichkeiten vereinfacht
wie folgt:
(u/2)/b + (b - u)/b = S2, die Wahrscheinlichkeit des Sieges der Mannschaft 2.
(u/2)/a + (a - u)/a = N1, die Wahrscheinlichkeit der Niederlage der Mannschaft 1, folglich
1 - N1 = 1 - (u/2)/a - (a - u)/a = S1, die Wahrscheinlichkeit des Sieges der Mannschaft 1.
Die Vereinfachung in dieser Berechnung besteht darin, daß von gleichen Streubreiten der Zufallsfaktoren in beiden
Mannschaften ausgegangen wird. Diese Vereinfachung wird sichtbar, wenn man die Siegeswahrscheinlichkeiten beider Mannschaften
addiert, wobei man selbstverständlich 1 erhalten muß, also
(u/2)/b + (b - u)/b + 1 - (u/2)/a - (a - u)/a = 1.
Nach Überrechnung dieser Beziehung erhält man a = b.
Die Vereinfachung ist aber legitim, weil zwei Mannschaften mit ähnlichem Leistungspotential, die zur gleichen Zeit am gleichen
Ort spielen, auch unter den gleichen Bedingungen spielen. Der Unterschied, der sich aus der Kategorie Heimspiel/Auswärtsspiel
ergeben könnte, ist für die Streubreite der Zufallsfaktoren von geringem Gewicht.
Aus den oben abgeleiteten Ausdrücken läßt sich nun sehen, daß die Wahrscheinlichkeit des Sieges der
leistungsstärkeren Mannschaft zwischen 0,5 und 1 liegt.
1 entsteht für die leistungsstärkere Mannschaft, wenn die Leistungspotentiale
so unterschiedlich sind, daß die Zufallsstreubreiten sich nicht überschneiden, wenn also u = 0 ist. Für die andere Mannschaft
ist dann die Wahrscheinlichkeit der Niederlage gleich 1, daß heißt, die Wahrscheinlichkeit des Sieges gleich 0.
0,5 entsteht, wenn die Leistungspotentiale als gleich angesehen werden können, so daß u = a = b ist.
Der Sinn dieser Rechnung besteht nun in der Erkenntnis, daß der Sieg der einen oder der anderen Mannschaft nicht nur von
den Leistungspotentialen L1 und L2 abhängig ist, sondern von einer relativ großen Zufallsspanne getragen wird, die umso
größer wird, je näher die Leistungspotentiale beieinander liegen. Schließlich erkennt man daraus, daß
für Sieg oder Niederlage eben wegen dieser Zusammenhänge weder der Trainer noch die Spieler maßgeblich verantwortlich
gemacht werden können. Fußball ist und bleibt ein Spiel, in dem man mit einem relevanten Zufallspotential rechnen
muß. Wäre dies nicht so, hätte zum Beispiel Fußballtoto keinerlei Perspektive, weil jeder aufmerksame
Beobeachter dann den Sieger exakt vorherbestimmen könnte. Übrig bliebe eine Wette von Fachleuten gegen Laien,
in der letztere immer verlieren würden.
Nachtrag vom 08.02.2005: Im Angesicht der jüngsten Skadale um die Spielemanipulierung muß zwingend hinzugefügt werden, daß die obigen Darstellungen nur gültig sind, wenn alle Beteiligten, also Spieler und Schiedsrichter, gewissenhaft nach ehrlichen Kriterien gemäß ihren Möglichkeiten handeln.